Money can grow quietly in the background if you give it time. This magic is called compound interest. In this blog, we will understand how compound interest works explained simply, using easy words, clear examples, and step-by-step calculations.
By the end, you will know:
- What simple interest is
- What compound interest is
- The main formula of compound interest
- How to calculate it with real examples
- How it helps in savings and investments
- How it can hurt you in loans and credit cards
- Smart tips to use compound interest in your favour
First, Understand Simple Interest
Before learning compound interest, we must know simple interest.
Simple interest is interest calculated only on the original amount (principal).
Simple Interest Formula
Simple Interest=P×r×t
Where:
- P = Principal (starting money)
- r = Interest rate per year (in decimal, e.g., 5% = 0.05)
- t = Time in years
Example of Simple Interest
You invest $1,000 at 5% simple interest per year for 3 years.
Simple Interest=1000×0.05×3=150
- Interest earned in 3 years = $150
- Total amount after 3 years = $1,000 + $150 = $1,150
Here, every year the interest is calculated only on $1,000, not on the growing balance.
What Is Compound Interest?
Now, let’s come to the main topic: how compound interest works explained simply.
Compound interest means:
You earn interest on the principal and also on the interest that was added earlier.
In simple words, it is “interest on interest”.
Because of this, your money does not grow in a straight line. It grows faster with time, almost like going up a curve.
Basic Example (Yearly): How Compound Interest Works Explained Simply
Let’s take a very easy example.
- Principal (P) = $1,000
- Interest rate (r) = 5% per year
- Time = 3 years
- Compounding = once per year (annually)
Year 1
- Interest = 5% of $1,000 =
1000×0.05=50 - New balance = $1,000 + $50 = $1,050
Year 2
Now interest is on $1,050, not just $1,000.
- Interest = 5% of $1,050 =
1050×0.05=52.50 - New balance = $1,050 + $52.50 = $1,102.50
Year 3
Interest is now on $1,102.50.
- Interest = 5% of $1,102.50 =
1102.50×0.05=55.125 - New balance ≈ $1,102.50 + $55.13 ≈ $1,157.63
So, after 3 years with compound interest:
- Total amount ≈ $1,157.63
- Total interest earned ≈ $157.63
Compare this with simple interest:
- Simple interest after 3 years = $150
- Compound interest after 3 years ≈ $157.63
You earned extra interest because your interest from earlier years also started earning interest.
The Compound Interest Formula
There is a formula that helps you quickly calculate how compound interest works, without doing year-by-year calculations.
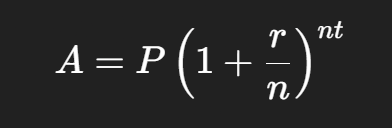
Where:
- A = Amount after time
- P = Principal (starting money)
- r = Annual interest rate (decimal form)
- n = Number of times interest is compounded per year
- t = Time in years
What is “n”?
- If interest is added once per year, then n=1
- If every 6 months (semi-annually), then n=2
- If every 3 months (quarterly), then n=4
- If every month, then n=12
- If every day, then n=365 (for most banks)
Example: Annual Compounding (Once Per Year)
Use the same example:
- P=1000
- r=5%=0.05
- n=1(once per year)
- t=3 =3 years
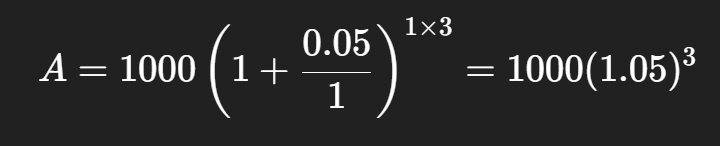
Now calculate(1.05)^3:
- 1.05^2 = 1.1025
- 1.05^3 = 1.1025×1.05=1.157625
A=1000×1.157625≈1157.63
This matches our year-by-year calculation.
How Compounding Frequency Changes the Result
One important part of how compound interest works explained simply is understanding how often the interest is added.
Let’s keep:
- P=1000
- r=5%=0.05
- t=5 years
We will change only n.
(a) Annual Compounding (n = 1)
A = 1000 (1 + 0.05)^5 =1000(1.05)5
Approximate:
- 1.05^2=1.1025
- 1.05^4 = (1.1025)^2 ≈ 1.21550625
- 1.05^5 =1.21550625×1.05≈1.27628
A≈1000×1.27628≈1276.28
So, amount ≈ $1,276.28
Interest earned ≈ $276.28
(b) Quarterly Compounding (n = 4)
Now interest is added 4 times a year.
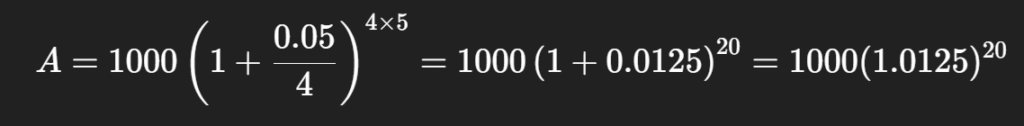
We won’t do every tiny step, but using exponent rules,
(1.0125)^{20} is a bit larger than 1.27628.
So, amount may be around $1,280+ (slightly higher than annual compounding).
(c) Monthly Compounding (n = 12)
Here again, we get a slightly higher final amount than quarterly.
The main idea:
More frequent compounding = more growth, but the difference is small for normal interest rates and time periods. Over very long times, the difference becomes bigger.
How Compound Interest Helps Your Savings
Compound interest is very helpful when you are:
- Saving money in a bank
- Investing in mutual funds, stocks, or retirement plans
- Keeping money for long-term goals (education, home, retirement)
Example: Long-Term Savings
You invest $2,000 at 8% compound interest per year, for 10 years, compounded once per year.
- P=2000
- r=8%=0.08
- n=1
- t=10
A=2000 (1 + 0.08)^{10} = 2000 (1.08)^{10}
Let’s approximate(1.08)^{10}:
- 1.08^2 ≈ 1.1664
- 1.08^4 ≈ 1.1664^2 ≈ 1.3605
- 1.08^5 ≈ 1.3605×1.08≈1.4693
- 1.08^{10} = (1.08^5)^2 ≈ 1.4693^2 ≈ 2.158
A≈2000×2.158≈4316
So after 10 years, your $2,000 becomes about $4,316.
Here:
- Interest earned ≈ $2,316
- This is more than the original amount you invested!
This shows how powerful compound interest is over long periods.
The Power of Starting Early
Time is the most important factor in how compound interest works.
Let’s compare two people:
- Person A: Invests $1,000 every year from age 25 to 35 (10 years) at 8% interest, then stops adding money and just lets it grow.
- Person B: Starts later and invests $1,000 every year from age 35 to 55 (20 years) at 8% interest.
Even though Person B invests for more years, Person A can still end up with more money at age 55 because A started earlier. This is because A’s money had more time to grow with compound interest.
The lesson:
Start saving and investing as early as possible, even with small amounts.
How Compound Interest Can Hurt You (Loans & Credit Cards)
Compound interest is not always good. It can also work against you when you borrow money.
Example: Credit Card
Suppose:
- You owe $1,000 on a credit card
- Interest rate = 20% per year
- Interest is compounded monthly
- You do not pay anything for 3 years (not recommended in real life!)
Here:
- P=1000
- r=20%=0.20
- n=12
- t=3
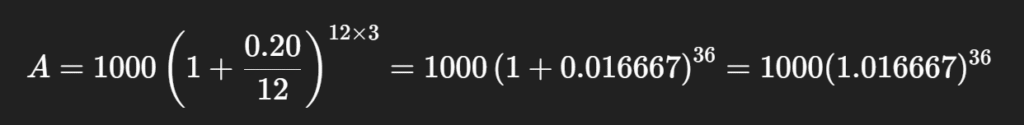
Approximate(1.016667)^{36}(we know it is more than(1.02)^{30}=1.81), so it might be near 1.81–1.90.
Let’s take approximate growth factor ≈ 1.81 (just for understanding):
A≈1000×1.81≈1810
So your $1,000 debt can grow to around $1,800+ if you do not pay it for 3 years.
This shows that high-interest debt with compound interest can grow very fast and become a big burden.
Difference Between Simple and Compound Interest (Quick View)
| Feature | Simple Interest | Compound Interest |
| Interest on | Only on principal | On principal + past interest |
| Growth style | Straight line | Curved, faster with time |
| Formula | ||
| Best for | Short-term loans, simple calculations | Long-term savings/investments |
| Can grow very large? | No | Yes, especially over long time |
| Effect on loans | Easier to manage | Can become heavy if rate is high |
Step-by-Step Example You Can Copy
Let’s do a full example slowly.
You invest $5,000 at 6% interest, compounded monthly, for 5 years.
Step 1: Identify values
- P=5000
- r=6%=0.06
- n=12(monthly)
- t=5
Step 2: Put into formula
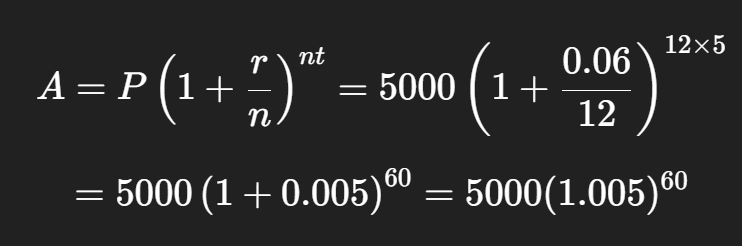
Step 3: Approximate the growth factor
We know:
- 1.005^{12}≈ 1.062 (roughly 6.2% per year)
- Over 5 years, 1.005^{60} = (1.005^{12})^5
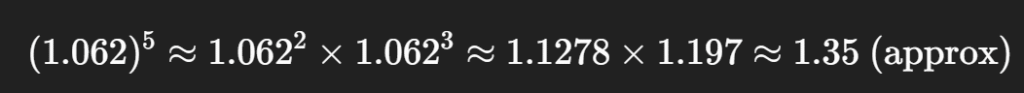
So,
A≈5000×1.35≈6750
Final amount ≈ $6,750
Interest earned ≈ $1,750
This is the power of compound interest over a few years.
Practical Tips to Use Compound Interest Wisely
Now that you understand how compound interest works explained simply, here are some practical tips:
1. Start Early
Even small amounts invested when you are young can grow a lot over time.
2. Invest Regularly
Try to add money every month or every year. Regular contributions plus compound interest can build a big amount.
3. Let Your Money Stay Invested
Avoid withdrawing your investment again and again. The longer it stays, the more time compound interest has to work.
4. Look for Better Returns (But Stay Safe)
A higher interest rate can grow your money faster. But do not take risky options you do not understand. Balance safety and returns.
5. Avoid High-Interest Debt
Credit card and personal loan rates are often very high. When compound interest works on high-interest debt, the amount you owe can grow quickly.
6. Pay Your Credit Card in Full
If you use a credit card, try to pay the full bill every month. This way, compound interest does not get a chance to increase your debt.
Short Summary
- Simple interest = interest only on the original principal.
- Compound interest = “interest on interest”.
- Formula:
- The more frequent the compounding and the longer the time, the more your money grows.
- It is very good for savings and investments.
- It is very dangerous for high-interest loans and credit cards if you do not pay them on time.
Also Read: General Investing vs Roth IRA: A Comparison with Examples
Conclusion
In this blog, we have seen how compound interest works explained simply using easy language, clear formulas, and live examples. Compound interest can be your best friend when you save and invest wisely, and your worst enemy when you ignore high-interest debts.
If you start early, invest regularly, and stay away from expensive loans, compound interest will quietly work in the background to grow your wealth over time. Even small steps today can make a big difference in your future.










